この記事では、簡単なニューラルネットワークをスクラッチで実装します。
特にバックプロパゲーションの実装は、数式の通りそのままコードにするのではなく配列の転置や順番の入れ替えなどが必要なので、ゼロから実装しようとすると非常に迷うところです。
今回はこのバックプロパゲーションの実装の考え方に焦点を当てて解説します。

学習するデータ：XOR回路

今回は、2つの入力値（0か1）を受け取って1つの値を出力する論理回路のうち、XOR（排他的論理和）回路を解く問題として説明します。
XOR回路は、2つの入力値が同じ場合は0を、違う場合は1を出力します。つまり、次の表のような回路になります。

今回は、ニューラルネットワークによって上記の回路を学習し、入力から出力を予測できるようにします。つまり、2つの値を持つ4つのデータが学習データとなり、入力ユニットが2つの二値分類モデルを作ります。

ニューラルネットワークによる実装

ここでは次のようなシンプルなニューラルネットワークで、XOR回路を学習します。

2つの入力と1つの出力の間に、3つのユニットを持つ隠れ層を配置しています。
隠れ層と出力層の活性化関数をシグモイド関数として、このネットワークのフォワードプロパゲーション（順伝播）を式で書くと

です。このように出力値（予測値）を出せたら、予測値と正解ラベルとの誤差を以下のコスト関数で計算します。

コスト関数まで計算できたら、次はバックプロパゲーションによって各パラメータに関するコスト関数の勾配を求めます。
それぞれの勾配の値がどのようになるか、ここでは結果だけ示すので、導出過程が知りたい人は後でこちらの記事を見てみてください。

各パラメータに関するコスト関数の勾配を求められたら、勾配降下法によってパラメータの値を更新します。

以上がニューラルネットワークの流れになります。

この一連の流れをPythonで実装すると、次のようなプログラムになります。
実行すると学習が行われ、完了後に予測値が表示されるので、だいたい正しいXOR回路に近い値が出力されることを確認してください。

import numpy as np

import matplotlib.pyplot as plt



#ニューラルネットワークのモデル

input_size = 2

hidden_size = 3

output_size = 1



#重みパラメータの定義

w1 = np.random.uniform(low=-1, high=1, size=(input_size, hidden_size))

b1 = np.zeros((1, hidden_size))

w2 = np.random.uniform(low=-1, high=1, size=(hidden_size, output_size))

b2 = np.zeros((1, output_size))



#活性化関数とその微分

def sigmoid(x):

    y = 1 / (1 + np.exp(-x))

    return y



def sigmoid_derivative(x):

    y = sigmoid(x) * (1-sigmoid(x))

    return y



# データセット（XOR）

x = np.array([[0,0], [0,1], [1,0], [1,1]])

y = np.array([[0], [1], [1], [0]])

m = x.shape[0]


# 学習率

learning_rate = 0.2

# エポック 

epochs =  100000

#目的関数の出力の値を保持するリスト

cost = [] 



#学習ループ

for _ in range(epochs):



    # フォワードプロパゲーション

    z1 = np.dot(x, w1)  + b1

    a1 = sigmoid(z1)

    z2 = np.dot(a1, w2) + b2 

    a2 = sigmoid(z2)



    # コスト関数

    cost.append(- np.sum(y * np.log(a2) + (1-y) * np.log(1 - a2)) / m )

    

    # バックプロパゲーション

    derivative_z2 = (a2 - y) / m

    delta_w2 = np.dot(a1.T, derivative_z2)

    delta_b2 = np.sum(derivative_z2, axis=0 ,keepdims=True)

    derivative_z1 = np.dot(derivative_z2, w2.T) * sigmoid_derivative(z1)

    delta_w1 = np.dot(x.T, derivative_z1)

    delta_b1 = np.sum(derivative_z1, axis=0 ,keepdims=True)

    

    # パラメータ更新

    w1 = w1 - learning_rate * delta_w1

    b1 = b1 - learning_rate * delta_b1

    w2 = w2 - learning_rate * delta_w2

    b2 = b2 - learning_rate * delta_b2



#学習完了



#コスト関数の値の推移をプロット

plt.plot(cost)

plt.ylabel("cost")

plt.xlabel("epochs")

plt.show()





#学習後のパラメータを使って予測

z1 = np.dot(x, w1)  + b1

a1 = sigmoid(z1)

z2 = np.dot(a1, w2) + b2 

a2 = sigmoid(z2)



print("予測値：\\n", a2)

バックプロパゲーションの実装の考え方を解説

上の実装の中から、バックプロパゲーションの部分を取り出して、改めて式と対応付けて見てみましょう。

式とコードを見比べると、コードの方では転置が入っていたり、かける順番が式と変わっている部分があるのがわかると思います。さらに、バイアスに関する勾配では、np.sumで総和を取っています。
なぜこのようにするのか、ゼロから自分で実装するとなると何を基に考えていいかわからないかもしれません。
何を求めたいかを考えることでわかってくると思うので、ここから解説します。
その前に、まず前提としてわかっていてほしいことが2つあります。

1. 求めたい配列の形

まず、各勾配は、以下のようにコスト関数の値を各要素で微分したものになります。

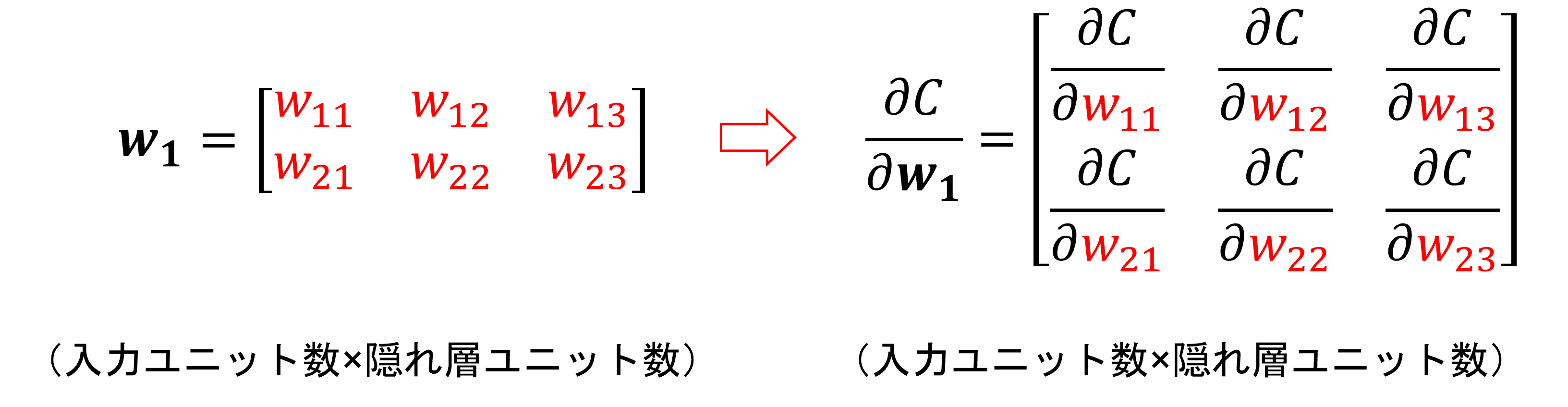
よって各パラメータに関する勾配は、対応するパラメータと同じ形の配列になるはずです。
つまり、各勾配は次の形の配列になる必要があります。

2. 行列積の意味

もう1つは、行列積の計算の意味についてです。
行列同士の積を計算する時、左側の行列の列数と右側の行列の行数が一致していないと計算できないことは知っていると思います。
これについてもう少し詳しく考えてみましょう。

このように行列積を見てみると、左側の行列の列方向（横方向）、および右側の行列の行方向（縦方向）に総和を取っていることがわかります。（当然、他の要素についても同じです。）

その上で、先ほどの\( \frac{\partial C}{\partial \boldsymbol{w_1}} \)の計算を見てみましょう。

\( \frac{\partial C}{\partial \boldsymbol{z_1}} \)の形は（データ数×隠れ層ユニット数）、\( \boldsymbol{x} \)の形は（データ数×入力ユニット数）なので、そのままでは計算できません。
さらに、「1. 求めたい配列の形」より、\( \frac{\partial C}{\partial \boldsymbol{w_1}} \)の形は（入力ユニット数×隠れ層ユニット数）になる必要があります。
よって、\( \boldsymbol{x} \)を転置して、順番を入れ替えることで、（入力ユニット数×データ数）・（データ数×隠れ層ユニット数）となり、正しい計算になります。そしてこれは、データ数方向に総和を取っているということがわかると思います。

以上の2点を踏まえて、各勾配の実装について順に見ていきましょう。

・derivative_z2

\( \boldsymbol{a_2} \)と\( \boldsymbol{y} \)はどちらも（データ数×出力ユニット数）なので、そのまま計算すればいいです。

・delta_w2

\( \frac{\partial C}{\partial \boldsymbol{z_2}} \)は（データ数×出力ユニット数）、\( \boldsymbol{a_1} \)は（データ数×隠れ層ユニット数）なので、\( \boldsymbol{a_1} \)を転置して順番を入れ替えることで、データ数方向に総和を取り、（隠れ層ユニット数×出力ユニット数）という結果が得られます。

・delta_b2

\( \frac{\partial C}{\partial \boldsymbol{z_2}} \)は（データ数×出力ユニット数）なので、「np.sum」でデータ数方向（axis=0）に総和を取ることで、（1×出力ユニット数）という結果が得られます。

・derivative_z1

まず前半の\( \frac{\partial C}{\partial \boldsymbol{z_2}}・\boldsymbol{w_2} \)の部分です。\( \frac{\partial C}{\partial \boldsymbol{z_2}} \)は（データ数×出力ユニット数）、\( \boldsymbol{w_2} \)は（隠れ層ユニット数×出力ユニット数）なので、\( \boldsymbol{w_2} \)を転置することで（データ数×隠れ層ユニット数）になるようにします。

後半部の\( g'(\boldsymbol{z_1}) \)は（データ数×隠れ層ユニット数）なので、前半部との要素ごとの積を取ります。
活性化関数に関する部分は、このように行列積ではなくアダマール積（同じ位置の要素同士の積）になります。順伝播において、活性化関数は配列の各要素ごとに適用するだけなので、逆伝播でもそうなることが直観的にわかると思います。

・delta_w1

\( \frac{\partial C}{\partial \boldsymbol{z_1}} \)は（データ数×隠れ層ユニット数）、\( \boldsymbol{x} \)は（データ数×入力ユニット数）なので、\( \boldsymbol{x} \)を転置して順番を入れ替えることで、データ数方向に総和を取り、（入力ユニット数×隠れ層ユニット数）という結果が得られます。

・delta_b1

\( \frac{\partial C}{\partial \boldsymbol{z_1}} \)は（データ数×隠れ層ユニット数）なので、「np.sum」でデータ数方向（axis=0）に総和を取ることで、（1×隠れ層ユニット数）という結果が得られます。

まとめ

以上がバックプロパゲーションの実装の組み立て方になります。
式で書くのと実装とで違いがありますが、その意味がわかったでしょうか。ただ計算ができればいいのではなく、それぞれの式がどういう計算をしたいのかを考えて実装しなければいけません。
実用上は既存のライブラリを使うと思うのでここまで考えることはありませんが、その中でどういう計算が行われているかも、ぜひ知っておきましょう。